CNN - Part 2¶
AlexNet (2012)¶
- "ImageNet Classification with Deep Convolutional Neural Networks"
- Alex Krizhevsky, Ilya Sutskever, and Geoffrey Hinton created a “large, deep convolutional neural network” that was used to win the 2012 ILSVRC (ImageNet Large-Scale Visual Recognition Challenge).
- 2012 marked the first year where a CNN was used to achieve a top 5 test error rate of 15.4%
- The next best entry achieved an error of 26.2%, which was an astounding improvement that pretty much shocked the computer vision community.
- 1000 categories

- Trained the network on ImageNet data, which contained over 15 million annotated images from a total of over 22,000 categories.
- Used ReLU for the nonlinearity functions.
- Used data augmentation techniques that consisted of image translations, horizontal reflections, and patch extractions.
- Implemented dropout layers in order to combat the problem of overfitting to the training data.
- Trained the model using batch stochastic gradient descent, with specific values for momentum and weight decay.
- Trained on two GTX 580 GPUs for five to six days.
The neural network developed by Krizhevsky, Sutskever, and Hinton in 2012 was the coming out party for CNNs in the computer vision community. This was the first time a model performed so well on a historically difficult ImageNet dataset. Utilizing techniques that are still used today, such as data augmentation and dropout, this paper really illustrated the benefits of CNNs and backed them up with record breaking performance in the competition.
ZF Net (2013)¶
https://arxiv.org/pdf/1311.2901v3.pdf
- “Visualizing and Understanding Convolutional Neural Networks”
- Matthew Zeiler and Rob Fergus
- 11.2% error rate
- fine tuning to the previous AlexNet structure
- explaining a lot of the intuition behind ConvNets and showing how to visualize the filters and weights correctly
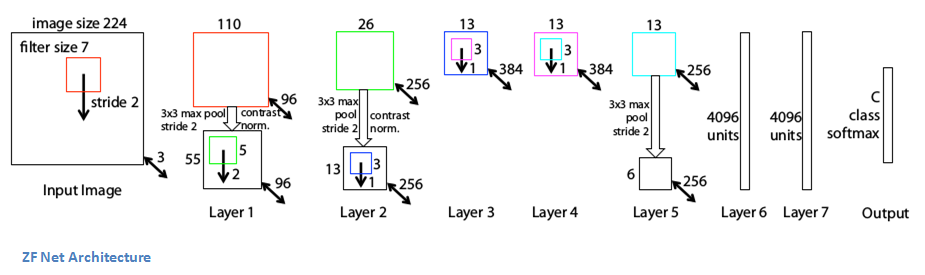
- Very similar architecture to AlexNet, except for a few minor modifications.
- AlexNet trained on 15 million images, while ZF Net trained on only 1.3 million images.
- Instead of using 11x11 sized filters in the first layer (which is what AlexNet implemented), ZF Net used filters of size 7x7 and a decreased stride value. The reasoning behind this modification is that a smaller filter size in the first conv layer helps retain a lot of original pixel information in the input volume. A filtering of size 11x11 proved to be skipping a lot of relevant information, especially as this is the first conv layer.
- As the network grows, we also see a rise in the number of filters used.
- Used ReLUs for their activation functions, cross-entropy loss for the error function, and trained using batch stochastic gradient descent.
- Trained on a GTX 580 GPU for twelve days.
- Developed a visualization technique named Deconvolutional Network, which helps to examine different feature activations and their relation to the input space. Called “deconvnet” because it maps features to pixels (the opposite of what a convolutional layer does).
DeConvNet¶
The basic idea behind how this works is that at every layer of the trained CNN, you attach a “deconvnet” which has a path back to the image pixels. An input image is fed into the CNN and activations are computed at each level. This is the forward pass. Now, let’s say we want to examine the activations of a certain feature in the 4th conv layer. We would store the activations of this one feature map, but set all of the other activations in the layer to 0, and then pass this feature map as the input into the deconvnet. This deconvnet has the same filters as the original CNN. This input then goes through a series of unpool (reverse maxpooling), rectify, and filter operations for each preceding layer until the input space is reached.


VGG Net (2014)¶
https://arxiv.org/pdf/1409.1556v6.pdf
- "VERY DEEP CONVOLUTIONAL NETWORKS FOR LARGE-SCALE IMAGE RECOGNITION"
- Karen Simonyan and Andrew Zisserman
- 7.3% error rate.
- Simplicity and depth. 19 layer CNN that strictly used 3x3 filters with stride and pad of 1, along with 2x2 maxpooling layers with stride 2.
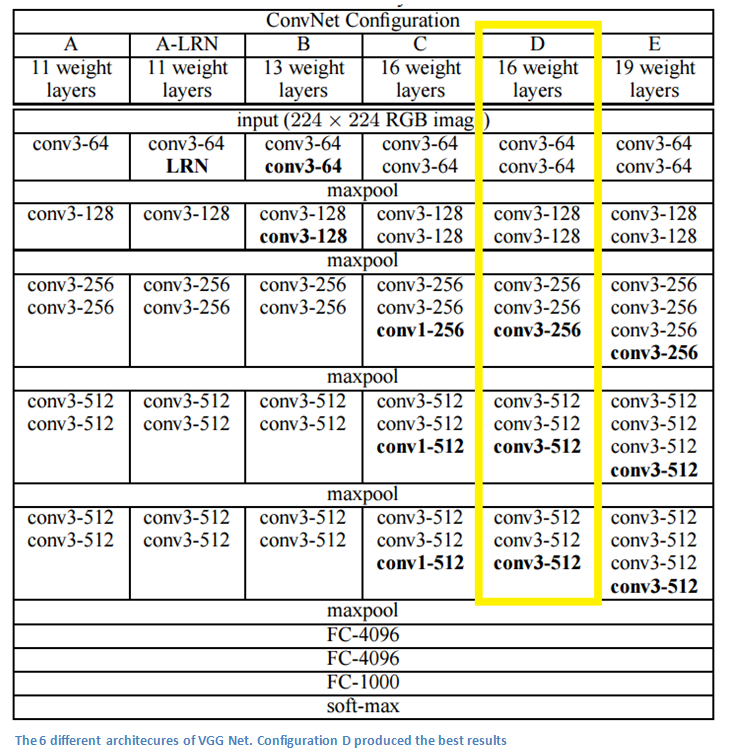
- The use of only 3x3 sized filters is quite different from AlexNet’s 11x11 filters in the first layer and ZF Net’s 7x7 filters. The authors’ reasoning is that the combination of two 3x3 conv layers has an effective receptive field of 5x5. This in turn simulates a larger filter while keeping the benefits of smaller filter sizes. One of the benefits is a decrease in the number of parameters. Also, with two conv layers, we’re able to use two ReLU layers instead of one.
- 3 conv layers back to back have an effective receptive field of 7x7.
- As the spatial size of the input volumes at each layer decrease (result of the conv and pool layers), the depth of the volumes increase due to the increased number of filters as you go down the network.
- Interesting to notice that the number of filters doubles after each maxpool layer. This reinforces the idea of shrinking spatial dimensions, but growing depth.
- Worked well on both image classification and localization tasks. The authors used a form of localization as regression (see page 10 of the paper for all details).
- Built model with the Caffe toolbox.
- Used scale jittering as one data augmentation technique during training.
- Used ReLU layers after each conv layer and trained with batch gradient descent.
- Trained on 4 Nvidia Titan Black GPUs for two to three weeks.
GoogLeNet (2015)¶
- "Going Deeper with Convolutions"
- No simplicity - Inception module.
- 22 layers
- ILSVRC 2014 winner with a top 5 error rate of 6.7%
- Refference: [1] Know your meme: We need to go deeper. http://knowyourmeme.com/memes/we-need-to-go-deeper.

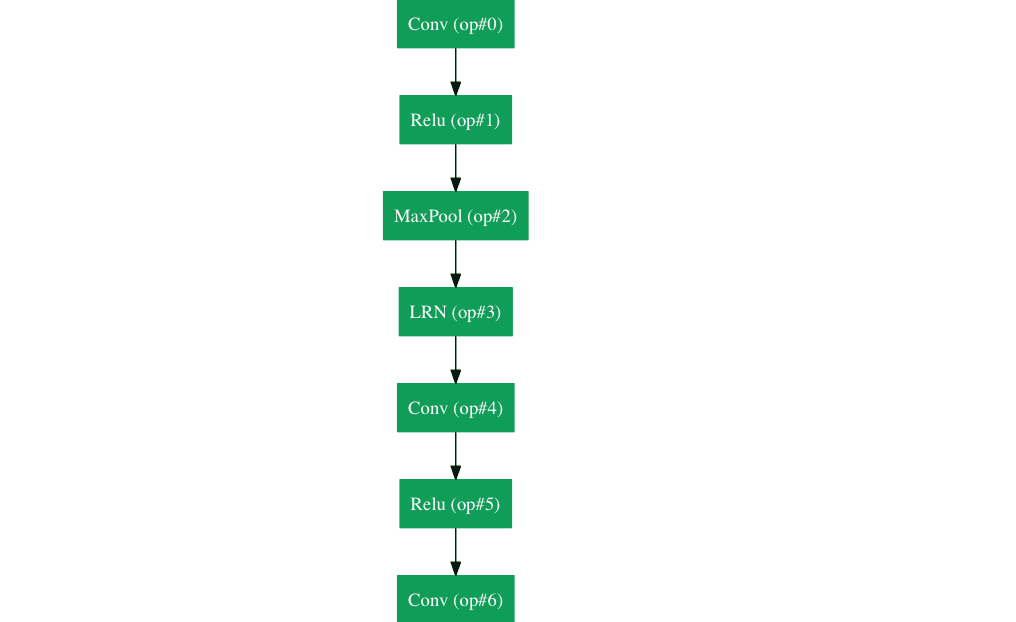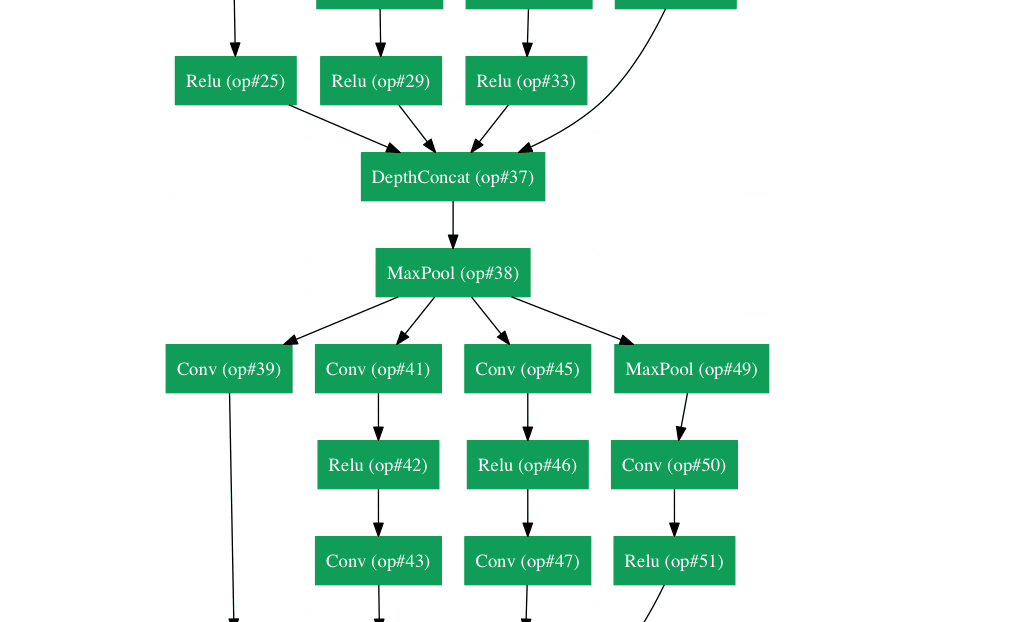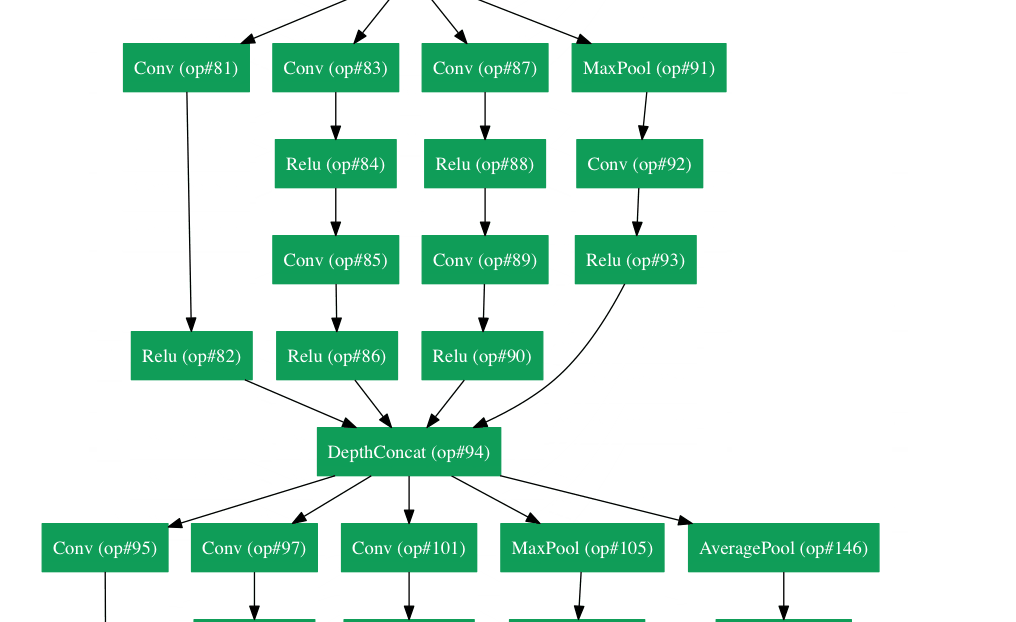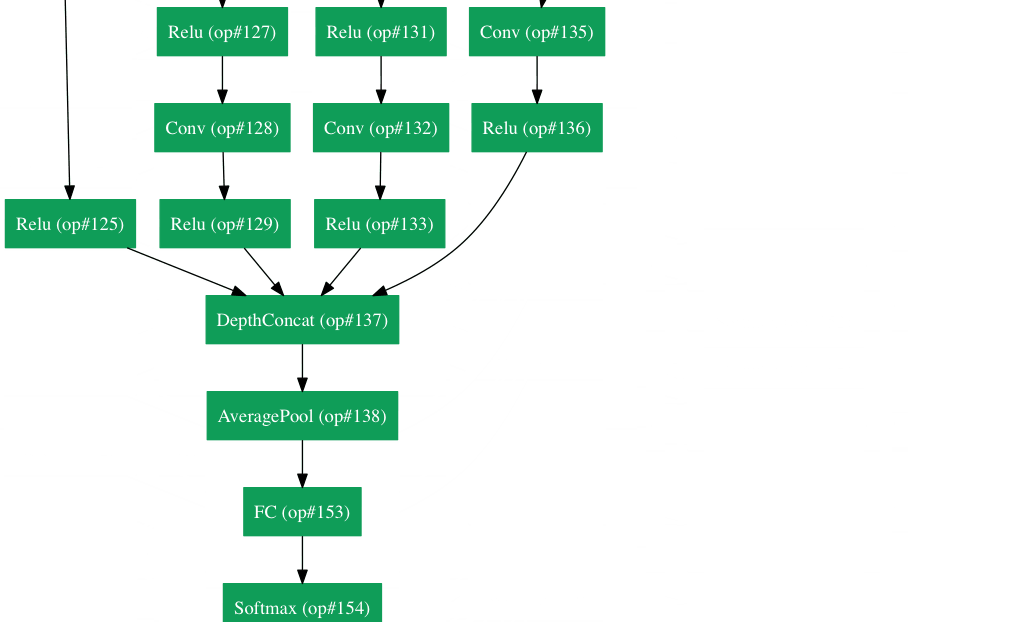
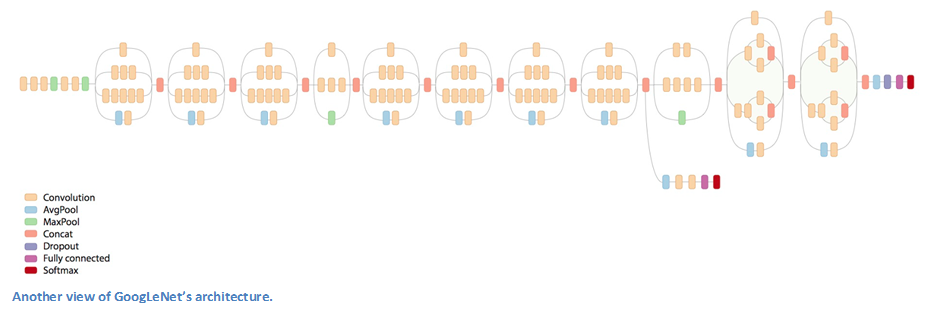
Inception Module¶
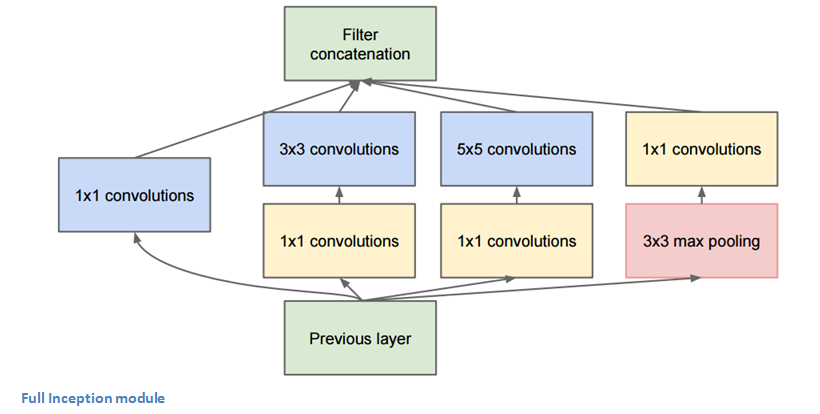
The bottom green box is our input and the top one is the output of the model (Turning this picture right 90 degrees would let you visualize the model in relation to the last picture which shows the full network). Basically, at each layer of a traditional ConvNet, you have to make a choice of whether to have a pooling operation or a conv operation (there is also the choice of filter size). What an Inception module allows you to do is perform all of these operations in parallel. In fact, this was exactly the “naïve” idea that the authors came up with.
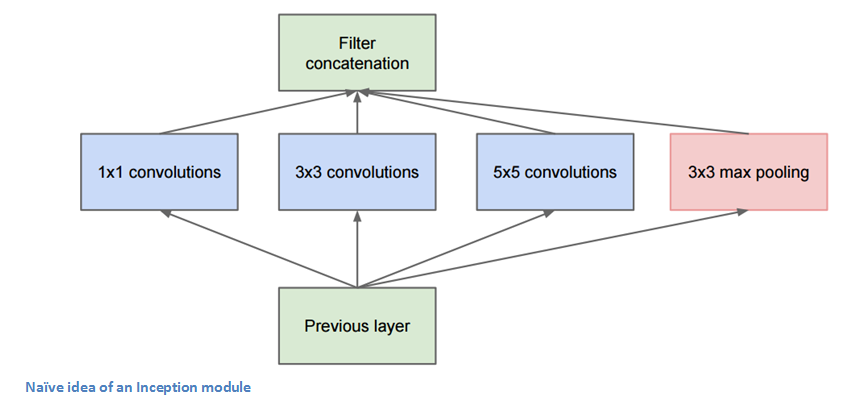
Now, why doesn’t this work? It would lead to way too many outputs. We would end up with an extremely large depth channel for the output volume. The way that the authors address this is by adding 1x1 conv operations before the 3x3 and 5x5 layers. The 1x1 convolutions (or network in network layer) provide a method of dimensionality reduction. For example, let’s say you had an input volume of 100x100x60 (This isn’t necessarily the dimensions of the image, just the input to any layer of the network). Applying 20 filters of 1x1 convolution would allow you to reduce the volume to 100x100x20. This means that the 3x3 and 5x5 convolutions won’t have as large of a volume to deal with. This can be thought of as a “pooling of features” because we are reducing the depth of the volume, similar to how we reduce the dimensions of height and width with normal maxpooling layers. Another note is that these 1x1 conv layers are followed by ReLU units which definitely can’t hurt (See Aaditya Prakash’s great post for more info on the effectiveness of 1x1 convolutions). Check out this video for a great visualization of the filter concatenation at the end.
You may be asking yourself “How does this architecture help?”. Well, you have a module that consists of a network in network layer, a medium sized filter convolution, a large sized filter convolution, and a pooling operation. The network in network conv is able to extract information about the very fine grain details in the volume, while the 5x5 filter is able to cover a large receptive field of the input, and thus able to extract its information as well. You also have a pooling operation that helps to reduce spatial sizes and combat overfitting. On top of all of that, you have ReLUs after each conv layer, which help improve the nonlinearity of the network. Basically, the network is able to perform the functions of these different operations while still remaining computationally considerate. The paper does also give more of a high level reasoning that involves topics like sparsity and dense connections.
Main Points
- Used 9 Inception modules in the whole architecture, with over 100 layers in total! Now that is deep…
- No use of fully connected layers! They use an average pool instead, to go from a 7x7x1024 volume to a 1x1x1024 volume. This saves a huge number of parameters.
- Uses 12x fewer parameters than AlexNet.
- During testing, multiple crops of the same image were created, fed into the network, and the softmax probabilities were averaged to give us the final solution.
- Utilized concepts from R-CNN for their detection model.
- There are updated versions to the Inception module (Versions 6 and 7).
- Trained on “a few high-end GPUs within a week”.
Why It’s Important
GoogLeNet was one of the first models that introduced the idea that CNN layers didn’t always have to be stacked up sequentially. Coming up with the Inception module, the authors showed that a creative structuring of layers can lead to improved performance and computationally efficiency. This paper has really set the stage for some amazing architectures that we could see in the coming years.
Microsoft ResNet (2015)¶
https://arxiv.org/pdf/1512.03385v1.pdf
- "Deep Residual Learning for Image Recognition"
- 152 layer architecture
- Set new records in classification, detection, and localization through one incredible architecture.
- ILSVRC 2015 with an incredible error rate of 3.6% (Depending on their skill and expertise, humans generally hover around a 5-10% error rate.
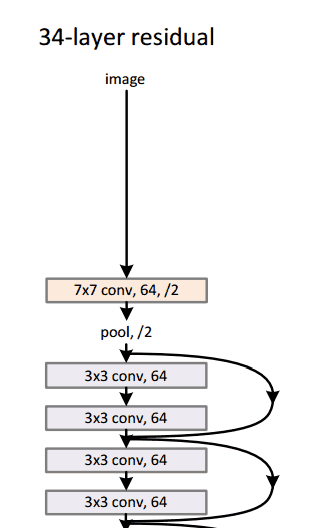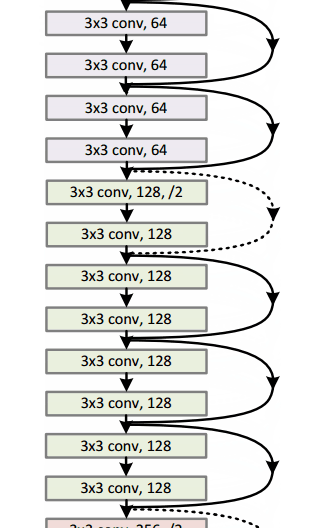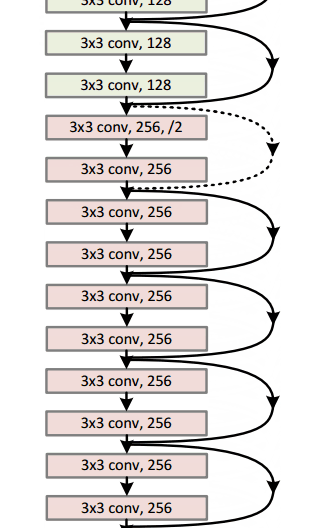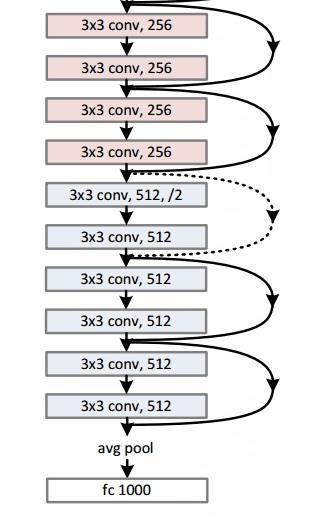
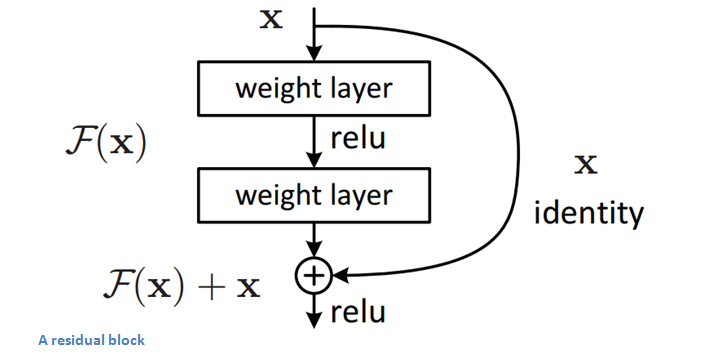
Residual Block¶
The idea behind a residual block is that you have your input x go through conv-relu-conv series. This will give you some F(x). That result is then added to the original input x. Let’s call that H(x) = F(x) + x. In traditional CNNs, your H(x) would just be equal to F(x) right? So, instead of just computing that transformation (straight from x to F(x)), we’re computing the term that you have to add, F(x), to your input, x. Basically, the mini module shown below is computing a “delta” or a slight change to the original input x to get a slightly altered representation (When we think of traditional CNNs, we go from x to F(x) which is a completely new representation that doesn’t keep any information about the original x). The authors believe that “it is easier to optimize the residual mapping than to optimize the original, unreferenced mapping”.
Another reason for why this residual block might be effective is that during the backward pass of backpropagation, the gradient will flow easily through the graph because we have addition operations, which distributes the gradient.
Main Points¶
- “Ultra-deep” – Yann LeCun.
- 152 layers…
- Interesting note that after only the first 2 layers, the spatial size gets compressed from an input volume of 224x224 to a 56x56 volume.
- Authors claim that a naïve increase of layers in plain nets result in higher training and test error (Figure 1 in the paper).
- The group tried a 1202-layer network, but got a lower test accuracy, presumably due to overfitting.
- Trained on an 8 GPU machine for two to three weeks.
Object Localization¶
- Additional 4 outputs:
x,y,width,height - Custom loss function using softmax and regression
Style Transfer¶
Generating Image Descriptions (2014)¶
https://arxiv.org/pdf/1412.2306v2.pdf
- "Deep Visual-Semantic Alignments for Generating Image Descriptions"
- Andrej Karpathy, Li Fei-Fei
- Combining CNN & bi-directional LSTM to generate natural language descriptions of different image regions.
- Input an image - outputs a text description.

Generative Adversarial Networks¶
https://arxiv.org/pdf/1312.6199v4.pdf
- Intriguing properties of neural networks (2014)

!wget https://i.ytimg.com/vi/SNggmeilXDQ/maxresdefault.jpg
Class Prediction using ResNet¶
from keras.applications.resnet50 import ResNet50
from keras.preprocessing import image
from keras.applications.resnet50 import preprocess_input, decode_predictions
import numpy as np
model = ResNet50(weights='imagenet')
img_path = 'maxresdefault.jpg'
img = image.load_img(img_path, target_size=(224, 224))
x = image.img_to_array(img)
x = np.expand_dims(x, axis=0)
x = preprocess_input(x)
preds = model.predict(x)
# decode the results into a list of tuples (class, description, probability)
# (one such list for each sample in the batch)
print('Predicted:', decode_predictions(preds, top=3)[0])

Extract features from an arbitrary intermediate layer with VGG19¶
from keras.applications.vgg19 import VGG19
from keras.preprocessing import image
from keras.applications.vgg19 import preprocess_input
from keras.models import Model
import numpy as np
base_model = VGG19(weights='imagenet')
base_model.summary()
model = Model(inputs=base_model.input, outputs=base_model.get_layer('block4_pool').output)
img_path = 'maxresdefault.jpg'
img = image.load_img(img_path, target_size=(224, 224))
x = image.img_to_array(img)
x = np.expand_dims(x, axis=0)
x = preprocess_input(x)
block4_pool_features = model.predict(x)
print(block4_pool_features.shape)
print(block4_pool_features)
Fine-tune InceptionV3 on a new set of classes¶
from keras.applications.inception_v3 import InceptionV3
from keras.preprocessing import image
from keras.models import Model
from keras.layers import Dense, GlobalAveragePooling2D
from keras import backend as K
# create the base pre-trained model
base_model = InceptionV3(weights='imagenet', include_top=False)
# add a global spatial average pooling layer
x = base_model.output
x = GlobalAveragePooling2D()(x)
# let's add a fully-connected layer
x = Dense(1024, activation='relu')(x)
# and a logistic layer -- let's say we have 200 classes
predictions = Dense(200, activation='softmax')(x)
# this is the model we will train
model = Model(inputs=base_model.input, outputs=predictions)
# first: train only the top layers (which were randomly initialized)
# i.e. freeze all convolutional InceptionV3 layers
for layer in base_model.layers:
layer.trainable = False
# compile the model (should be done *after* setting layers to non-trainable)
model.compile(optimizer='rmsprop', loss='categorical_crossentropy')
# train the model on the new data for a few epochs
# model.fit_generator(...)
# at this point, the top layers are well trained and we can start fine-tuning
# convolutional layers from inception V3. We will freeze the bottom N layers
# and train the remaining top layers.
# let's visualize layer names and layer indices to see how many layers
# we should freeze:
for i, layer in enumerate(base_model.layers):
print(i, layer.name)
# we chose to train the top 2 inception blocks, i.e. we will freeze
# the first 249 layers and unfreeze the rest:
for layer in model.layers[:249]:
layer.trainable = False
for layer in model.layers[249:]:
layer.trainable = True
# we need to recompile the model for these modifications to take effect
# we use SGD with a low learning rate
from keras.optimizers import SGD
model.compile(optimizer=SGD(lr=0.0001, momentum=0.9), loss='categorical_crossentropy')
# we train our model again (this time fine-tuning the top 2 inception blocks
# alongside the top Dense layers
# model.fit_generator(...)
Project suggestions:¶
- Image noice cleaning - сравнение на различни модели.
- AutoML - генериране на модели.
- Генериране на текстове за новини на български по зададени ключови думи. Генериране на текствое за песни.
- Генериране на музика. Генериране на изображения (style transfer)
- Spell, grammatical checker.
- Document summarisation.
- Nice visualization projects.
- Data extraction.
- Kaggle Competition.

